VGGNet网络介绍
VGG系列结构图,
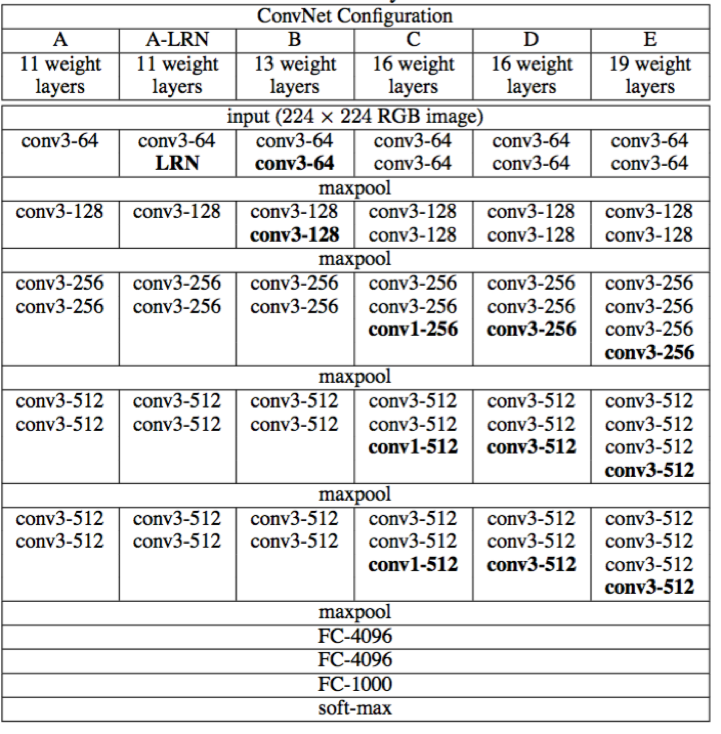
1,全部使用3*3的卷积核和2*2的池化核,通过不断加深网络结构来提升性能。
所有卷积层都是同样大小的filter:尺寸3x3,卷积步长Stirde = 1,填充Padding = 1
为什么这么搞?
A、3x3是最小的能够捕获左、右、上、下和中心概念的尺寸;
B、两个3x3的卷积层连在一起可视为5x5的filter,三个连在一起可视为一个7x7的
这是卷积的性质,受过#信号系统#这门课摧残的同学应该记忆犹新…
C、多个3x3的卷积层比一个大尺寸的filter卷积层有更多的非线性(多次经过非线性激活函数),使得判决函数更加具有判断性。
D、多个3x3的卷积层笔一个大尺寸的filter具有更少的参数。
2,实验过程中使用了1*1的卷积,其意义在于线性变换,不改变通道数,也不起降维作用(1*1卷积的降维作用等在Inception中才得到展现)。实际上1*1的卷积也是有效的,但是器效果并不如3*3的好,大的卷积核可以学习大的空间特征
3,有五段卷积操作,每段feature_map数目相同,越靠后数目越多,分别为64-128-256-512-512
4、 Multi-scale训练
首先对原始图片进行等比例缩放,使得短边要大于224,然后在图片上随机提取224x224窗口,进行训练。由于物体尺度变化多样,所以多尺度(Multi-scale)可以更好地识别物体。
方法1:在不同的尺度下,训练多个分类器:
参数S为短边长。训练S=256和S=384两个分类器,其中S=384的分类器用S=256的进行初始化,且将步长调为10e-3
方法2:直接训练一个分类器,每次数据输入的时候,每张图片被重新缩放,缩放的短边S随机从[256,512]中选择一个。
Multi-scale其实本身不是一个新概念,学过图像处理的同学都知道,图像处理中已经有这个概念了,我们学过图像金字塔,那就是一种多分辨率操作
只不过VGG网络第一次在神经网络的训练过程中提出也要来搞多尺寸。目的是为了提取更多的特征信息。像后来做分割的网络如DeepLab也采用了图像金字塔的操作。
5,LRN(局部响应归一化层)作用不大
6,网络越深越好
VGG_19结构示意图,
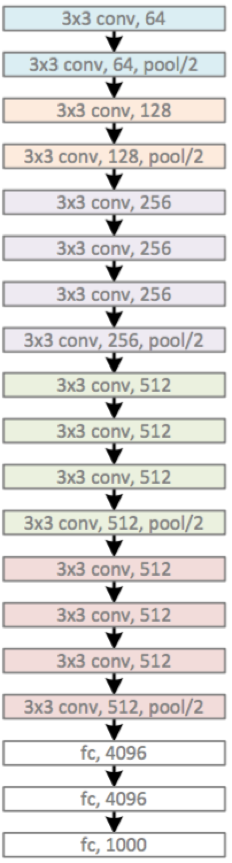
VGGNet测试代码
注,网络版本为VGG_16
# Author : Hellcat# Time : 2017/12/11import mathimport timeimport tensorflow as tffrom datetime import datetimedef conv_op(input_op, name, kh, kw, n_out, dh, dw, p): ''' 卷积层封装实现 核参数初始化使用了xavier方法 :param input_op:输入数据 :param name: 本层命名 :param kh: 卷积核高度 :param kw: 卷积核宽度 :param n_out: 输出 feature map 数量 :param dh: 高度方向步长 :param dw: 宽度方向步长 :param p: 变量收集器 :return: 输出层 ''' n_in = input_op.get_shape()[-1].value with tf.name_scope(name) as scope: kernel = tf.get_variable(scope+'w', shape=[kh,kw,n_in,n_out],dtype=tf.float32, initializer=tf.contrib.layers.xavier_initializer_conv2d()) conv = tf.nn.conv2d(input_op,kernel,(1,dh,dw,1),padding='SAME') bias_init_val = tf.constant(0.0, shape=[n_out],dtype=tf.float32) biases = tf.Variable(bias_init_val,trainable=True,name='b') z = tf.nn.bias_add(conv, biases) activation = tf.nn.relu(z,name=scope) p += [kernel, biases] return activationdef fc_op(input_op,name,n_out,p): ''' 全连接层封装实现 :param input_op:输入数据 :param name: 本层命名 :param n_out: 输出层节点数目 :param p: 变量收集器 :return: 输出层 ''' n_in = input_op.get_shape()[-1].value with tf.name_scope(name) as scope: kernel = tf.get_variable(scope+'w', shape=[n_in,n_out],dtype=tf.float32, initializer=tf.contrib.layers.xavier_initializer()) biases = tf.Variable(tf.constant(0.1,shape=[n_out], dtype=tf.float32),name='b') # relu_layer(x, weights, biases, name=None) # relu(matmul(x, weights) + biases) activation = tf.nn.relu_layer(input_op,kernel,biases,name=scope) p += [kernel,biases] return activationdef mpool_op(input_op,name,kh,kw,dh,dw): ''' 池化层封装实现 :param input_op: 输入数据 :param name: 本层命名 :param kh: 核高度 :param kw: 核宽度 :param dh: 高度方向步长 :param dw: 宽度方向步长 :return: 输出层 ''' return tf.nn.max_pool(input_op, ksize=[1,kh,kw,1], strides=[1,dh,dw,1], padding='SAME', name=name)def inference_op(input_op, keep_prob): ''' 网络实现 :param input_op: 输入数据 :param keep_prob: dropout参数 :return: 输出结果 ''' p=[] conv1_1 = conv_op(input_op,name='conv1_1',kh=3,kw=3,n_out=64,dh=1,dw=1,p=p) conv1_2 = conv_op(conv1_1,name='conv1_2',kh=3,kw=3,n_out=64,dh=1,dw=1,p=p) pool1 = mpool_op(conv1_2,name='pool1',kh=2,kw=2,dh=2,dw=2) conv2_1 = conv_op(pool1,name='conv2_1',kh=3,kw=3,n_out=128,dh=1,dw=1,p=p) conv2_2 = conv_op(conv2_1,name='conv2_2',kh=3,kw=3,n_out=128,dh=1,dw=1,p=p) pool2 = mpool_op(conv2_2,name='pool2',kh=2,kw=2,dh=2,dw=2) conv3_1 = conv_op(pool2,name='conv3_1',kh=3,kw=3,n_out=256,dh=1,dw=1,p=p) conv3_2 = conv_op(conv3_1,name='conv3_2',kh=3,kw=3,n_out=256,dh=1,dw=1,p=p) conv3_3 = conv_op(conv3_2,name='conv3_3',kh=3,kw=3,n_out=256,dh=1,dw=1,p=p) pool3 = mpool_op(conv3_3,name='pool3',kh=2,kw=2,dh=2,dw=2) conv4_1 = conv_op(pool3,name='conv4_1',kh=3,kw=3,n_out=512,dh=1,dw=1,p=p) conv4_2 = conv_op(conv4_1,name='conv4_2',kh=3,kw=3,n_out=512,dh=1,dw=1,p=p) conv4_3 = conv_op(conv4_2,name='conv4_3',kh=3,kw=3,n_out=512,dh=1,dw=1,p=p) pool4 = mpool_op(conv4_3,name='pool4',kh=2,kw=2,dh=2,dw=2) conv5_1 = conv_op(pool4,name='conv5_1',kh=3,kw=3,n_out=512,dh=1,dw=1,p=p) conv5_2 = conv_op(conv5_1,name='conv5_2',kh=3,kw=3,n_out=512,dh=1,dw=1,p=p) conv5_3 = conv_op(conv5_2,name='conv5_3',kh=3,kw=3,n_out=512,dh=1,dw=1,p=p) pool5 = mpool_op(conv5_3,name='pool5',kh=2,kw=2,dh=2,dw=2) shp = pool5.get_shape() flattened_shape = shp[1].value * shp[2].value * shp[3].value resh1 = tf.reshape(pool5,[-1,flattened_shape],name='resh1') fc6 = fc_op(resh1,name='fc6',n_out=4096,p=p) fc6_drop = tf.nn.dropout(fc6,keep_prob=keep_prob,name='fc6_drop') fc7 = fc_op(fc6_drop,name='fc7',n_out=4096,p=p) fc7_drop = tf.nn.dropout(fc7,keep_prob=keep_prob,name='fc7_drop') fc8 = fc_op(fc7_drop,name='fc8',n_out=1000,p=p) softmax = tf.nn.softmax(fc8) predictions = tf.argmax(softmax,axis=1) return predictions,softmax,fc8,pdef time_tensorflow_run(session, target, feed, info_string): ''' 网路运行时间测试函数 :param session: 会话对象 :param target: 运行目标节点 :param info_string:提示字符 :return: None ''' num_steps_burn_in = 10 # 预热轮数 total_duration = 0.0 # 总时间 total_duration_squared = 0.0 # 总时间平方和 for i in range(num_steps_burn_in + num_batches): start_time = time.time() _ = session.run(target, feed_dict=feed) duration = time.time() - start_time # 本轮时间 if i >= num_steps_burn_in: if not i % 10: print('%s: step %d, duration = %.3f' % (datetime.now(),i-num_steps_burn_in,duration)) total_duration += duration total_duration_squared += duration**2 mn = total_duration/num_batches # 平均耗时 vr = total_duration_squared/num_batches - mn**2 sd = math.sqrt(vr) print('%s:%s across %d steps, %.3f +/- %.3f sec / batch' % (datetime.now(), info_string, num_batches, mn, sd))def run_benchmark(): with tf.Graph().as_default(): image_size = 224 images = tf.Variable(tf.random_normal([batch_size,image_size,image_size,3], dtype=tf.float32, stddev=1e-1)) keep_prob = tf.placeholder(tf.float32) predictions,softmax,fc8,p = inference_op(images,keep_prob) init = tf.global_variables_initializer() sess = tf.Session() sess.run(init) time_tensorflow_run(sess,predictions,{keep_prob:1.0},'Forward') objective = tf.nn.l2_loss(fc8) # 模拟目标函数 grad = tf.gradients(objective, p) # 梯度求解 time_tensorflow_run(sess, grad,{keep_prob:0.5},'Forward-backward') # 反向传播batch_size = 32num_batches = 100run_benchmark() 输出如下面形式,我得机器实在是慢,进给出前几个输出示意,
'''
2017-12-12 11:06:03.731930: step 0, duration = 26.8372017-12-12 11:10:32.045152: step 10, duration = 26.878'''